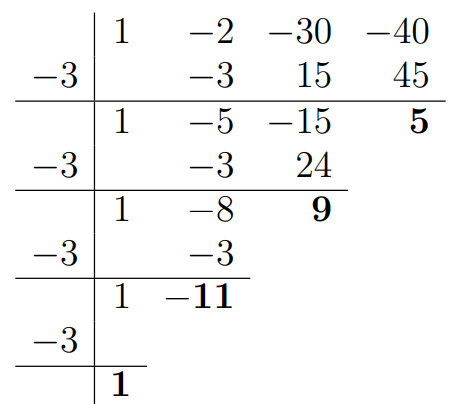Answers to Algebra Practical 4

$31OCT=25DEC⟹$ because 31 in base 8 is equal to 25 in base 10 ($8\cdot 3+1$)

Question 1 §

$$(2x+1)(3x^2+2)(4x^3+3)(5x^4+4)(6x^5+5)$$

$$⟹(2x\cdot 3x^2\cdot 4x^3\cdot 5x^4\cdot 6x^5)+\cdots +(1\cdot 2\cdot 3\cdot 4\cdot 5)$$

$$⟹720x^{15}+\cdots +120$$

$$\therefore \text{The degree is 15 and the constant term is 120.}$$

Question 2 §

$$2x^5+x^3-5x^2+2=(2x^2-1)q(x)+r(x)$$

Answers to Algebra Practical 4 2023-10-20 08.59.09.excalidraw So, by polynomial long division,

$$q(x)=x^3+x-\frac{5}{2},r(x)=x-\frac{1}{2}$$

$$LHS=RHS\therefore \text{valid solution}$$

Question 3 §

$$(3x^2+x-1)(2x^3-2x^2-x+2)-(x^3+2x^2-4x-11)(6x^2-x+9)$$

$$⟹(6x^5-6x^4+2x^4+\cdots )-(6x^5-x^4+12x^4+\cdots )$$

$$⟹(-4x^4+\cdots )-(11x^4+\cdots )$$

$$⟹-15x^4+\cdots$$

$$\therefore \text{Degree is 4 and the leading coefficient is -15.}$$

Question 4 §

$$4x^4-8x^3+6x^2+\frac{1}{2}x-\frac{15}{2}=(x-\frac{3}{2})q(x)+r(x)$$

$$⟹8x^4-16x^3+12x^2+x-15=2\left[(x-\frac{3}{2})q(x)+r(x)\right]$$

(1.5)	8	-16	12	1	-15
0	0	12	-6	9	15
	8	-4	6	10	0

$$\therefore 2q(x)=8x^3-4x^2+6x+10,2r(x)=0$$

$$⟹q(x)=4x^3-2x^2+3x+5,r(x)=0$$

$$\therefore \text{their quotient is }4x^3-2x^2+3x+5\text{, which is a mutiple of the quartic.}$$

Question 5 §

$$\frac{(x+3)(x^2-x-1)}{x^2+3x+4}=f(x)+\frac{g(x)}{h(x)}$$

$$⟹\frac{(x+3)(x^2-x-1)}{(x+3)(x+1)}=\frac{x^2-x-1}{x+1}=f(x)+\frac{g(x)}{h(x)}$$

Answers to Algebra Practical 4 2023-10-20 10.21.25.excalidraw

Thus, $f(x)=x-2,g(x)=1$:

$$\frac{(x+3)(x^2-x-1)}{x^2+3x+4}=f(x)+\frac{g(x)}{h(x)}:f(x)=x-2,g(x)=1,h(x)=x+1$$

$$\therefore x-2+\frac{1}{x+1}$$

Checking my answer §

$$x-2+\frac{1}{x+1}⟹\frac{(x-2)(x+1)+1}{x+1}⟹\frac{x^2-x-1}{x+1}$$

$$⟹\frac{x^2-x-1}{x+1}\cdot \frac{x+3}{x+3}⟹\frac{(x+3)(x^2-x-1)}{x^2+4x+3}$$

$$\text{Answer is incorrect - the initial denominator was factorised incorrectly.}$$

Correct answer §

$$\frac{(x+3)(x^2-x-1)}{x^2+3x+4}=f(x)+\frac{g(x)}{h(x)}$$

$$⟹\frac{(x+3)(x^2-x-1)}{x^2+3x+4}=\frac{f(x)h(x)+g(x)}{h(x)}\therefore h(x)=x^2+3x+4$$

$$⟹x^3+2x^2-4x-3=(x^2+3x+4)f(x)+g(x)$$

Answers to Algebra Practical 4 2023-10-20 10.39.44.excalidraw

$$\therefore f(x)=x-1,g(x)=-5x+1,h(x)=x^2+3x+4$$

Question 6 §

$$x^3-2x^2-30x-40=\cdots +c_2(x+3)+c_1(x+3)+c_0$$

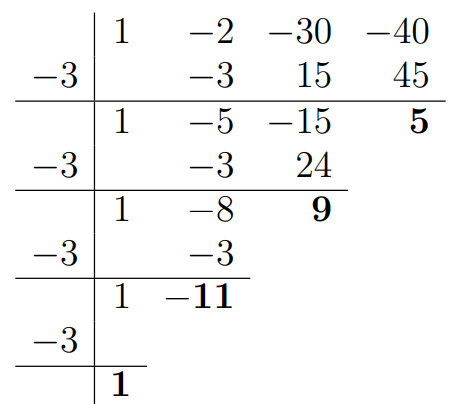
$$\therefore c_0=5,c_1=9,c_2=-11,c_3=1$$

Question 7 §

Factorise the following expressions as far as you can over $\mathbb{R}$, that is, using only real numbers:

Question A §

$$a^2+b^2-c^2-2ab$$

$$⟹(a+b{)}^2-c^2$$

$$⟹(a-b-c)(a-b+c)\text{ by difference of two squares}$$

Question B §

$$8x^3+b^6$$

$$⟹(b^2+2x)(b^4-2b^{2}x+4x^2)\text{ by inspcetion}$$

Question C §

$$x^8-a^8$$

$$⟹(x^4+a^4)(x^4-a^4)\text{ by difference of two squares}$$

$$⟹(x^4+a^4)(x^2+a^2)(x^2-a^2)\text{ by difference of two squares}$$

$$⟹(x^4+a^4)(x^2+a^2)(x+a)(x-a)\text{ by difference of two squares}$$

Question 8 §

$$(i)x^4+(-1+i)x^3+(-4-i)x^2+(-2-3i)x+(-6+3i)=[x-(-2+i)]q(x)+r(x)$$

(-2+i)	i	-1+i	-4-i	-2-3i	-6+3i
	0	-1-2i	5	-1+3i	6-3i
	i	-2-i	1-i	-3	0

$$⟹q(x)=i{x}^3-(2+i)x^2+(1-i)x-3,r(x)=0\therefore \text{factor}$$