Division with remainder for polynomials

Polynomials §

Definition: §

A polynomial is an expression of the form $f(x)=a_n{x}^n+\cdots +a_{1}x+a_0$, where $a_0,a_1,\dots ,a_n$ are coefficients from a field $F$. The variable $x$ is called the indeterminate.

Fields: §

Fields are sets of numbers where you can perform addition, subtraction, multiplication, and division (except by zero). Examples include:

• $\mathbb{Q}$: Rational numbers
• $\mathbb{R}$: Real numbers
• $\mathbb{C}$: Complex numbers

Historical Context: The concept of fields has been around for centuries, but the formal definition and study of fields as algebraic structures began in the 19th century.

Special Fields: §

• Field with Two Elements ($F_2$): This field consists of two symbols $\overline{0}$ and $\overline{1}$ which behave similarly to the integers 0 and 1, with the exception that $\overline{1}+\overline{1}=\overline{0}$. This is shown below in a Cayley table.

Degree of a Polynomial: §

The degree of a non-zero polynomial $f(x)$ is the largest integer $n$ such that $a_n\ne 0$. It’s denoted as $\text{deg}(f)$.

If $a_n=1$, then we call $f(x)$ monic. We also do not assume that $a_n\ne 0$ when we define a polynomial, we must state this.

A zero polynomial is a special case where we set $deg(0)=-\infty$ - this helps compact and simplify our definition for convention.

Operations on Polynomials: §

1. Addition: $(a_n{x}^n+\cdots +a_{1}x+a_0)+(b_n{x}^n+\cdots +b_{1}x+b_0)=(a_n+b_n)x^n+\cdots +(a_1+b_1)x+(a_0+b_0)$

2. Multiplication: $(a_n{x}^n+\cdots +a_{1}x+a_0)\cdot (b_m{x}^m+\cdots +b_{1}x+b_0)$ This involves using the distributive property and then collecting like terms.

The degrees of these operations are quite logical to deduce, where addition will simply be the maximum degree of either polynomial, and multiplication will be the sum of the degrees - due to the product rule with indices.

---

Polynomial Division with Remainder §

The Division Algorithm for $F[x]$: §

For any polynomials $f(x)$ and $g(x)$ in $F[x]$ with $g(x)\ne 0$, there exist unique polynomials $q(x)$ and $r(x)$ such that: $f(x)=g(x)q(x)+r(x)$ where either $r(x)=0$ or $\text{deg}(r(x))<\text{deg}(g(x))$.

Note however that there is no variant for polynomial division such as there is with integer division - apart from that, this is conceptually similar.

Historical Context: Polynomial division is an extension of the long division method used for integers. The division algorithm for polynomials is a foundational concept in algebra and has been studied for centuries.

Example: §

When dividing $f(x)=2x^4+x^2-x+1$ by $g(x)=2x-1$, we get: $q(x)=x^3+\frac{1}{2}{x}^2+\frac{3}{4}x-\frac{1}{8}$ and $r(x)=\frac{7}{8}$

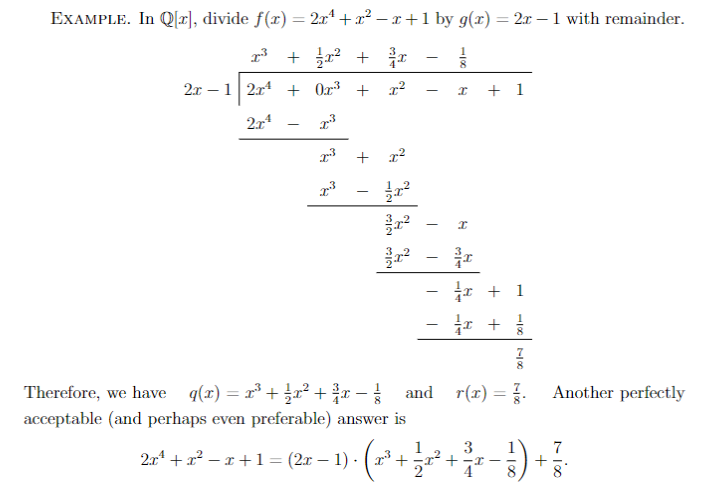
Proof of Uniqueness of $q(x)$ and $r(x)$ §

Given: We have two different ways of expressing the division of a polynomial $f(x)$ by another polynomial $g(x)$:

1. $f(x)=g(x)q(x)+r(x)$
2. $f(x)=g(x)q_1(x)+r_1(x)$

Both $r(x)$ and $r_1(x)$ satisfy the condition that either they are zero or their degree is less than the degree of $g(x)$.

Goal: Prove that $q_1(x)=q(x)$ and $r_1(x)=r(x)$.

Proof:

1. Combining the two given equations, we get: $g(x)q(x)+r(x)=f(x)=g(x)q_1(x)+r_1(x)$

2. Rearranging, we have: $g(x)[q_1(x)-q(x)]=r(x)-r_1(x)$

3. Now, consider the right-hand side, $r(x)-r_1(x)$. If this is non-zero, its degree would be less than the degree of $g(x)$ because both $r(x)$ and $r_1(x)$ have degrees less than $g(x)$.

4. On the left-hand side, if $g(x)[q_1(x)-q(x)]$ is non-zero, its degree would be $\text{deg}(g(x))+\text{deg}[q_1(x)-q(x)]$, which is at least $\text{deg}(g(x))$.

5. The contradiction arises when we realize that the left-hand side, if non-zero, would have a degree greater than or equal to $g(x)$, while the right-hand side would have a degree less than $g(x)$. This is impossible.

6. Thus, the only conclusion is that both sides of the equation are zero. This implies: $q_1(x)-q(x)=0⟹q_1(x)=q(x)$ $r(x)-r_1(x)=0⟹r(x)=r_1(x)$

This completes the proof of the uniqueness of $q(x)$ and $r(x)$.